戻る

Functional Names

函数の名前 その他 で以下のようなものが 有るようです。

TeX source code

では TeX ファイル （source code）を見てみます。

\documentclass[a5paper,12pt]{jarticle}
\begin{document}

\begin{table}
\caption{Function Names}
\label{tab:func}
\centering
\begin{tabular}{llll}
\textbackslash arccos & $\arccos$ & \textbackslash arcsin & $\arcsin$\\  
\textbackslash arctan & $\arctan$ & \textbackslash arg  & $\arg$\\ 
\textbackslash cos & $\cos$ & \textbackslash cosh & $\cosh$\\ 
\textbackslash cot & $\cot$ & \textbackslash coth &  $\coth$\\ 
\textbackslash csc & $\csc$ & \textbackslash deg &  $\deg$\\  
\textbackslash det & $\det$ &  \textbackslash dim & $\dim$\\
\textbackslash exp & $\exp$ &  \textbackslash gcd & $\gcd$\\  
\textbackslash hom & $\hom$ &  \textbackslash inf & $\inf$\\
\textbackslash ker & $\ker$ &  \textbackslash lg &  $\lg$\\
\textbackslash lim & $\lim$ &  \textbackslash liminf &  $\liminf$\\ 
\textbackslash limsup & $\limsup$ &  \textbackslash ln & $\ln$\\  
\textbackslash log & $\log$ &  \textbackslash max &  $\max$\\
\textbackslash min & $\min$ &  \textbackslash Pr & $\Pr$\\ 
\textbackslash sec & $\sec$ &  \textbackslash sin & $\sin$\\  
\textbackslash sinh & $\sinh$ & \textbackslash sup & $\sup$\\ 
\textbackslash tan & $\tan$ & \textbackslash tanh &  $\tanh$\\   
\end{tabular}
\end{table}

\end{document}

基本的に ”\func” を ”$\func$”の様に ”$”と”$”で囲みます

函数の表示例 その１

”sin”、”cos”、 等を 使用して” complex number” 複素数 表現

TeX source code

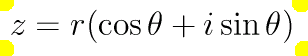
では TeX ファイル （source code）を見てみます。

\documentclass[a5paper,12pt]{jarticle}
\begin{document}
\begin{displaymath}
z = r(\cos\theta + i\sin\theta)
\end{displaymath}
\end{document}

函数の表示例 その２

厳密に 函数？では有りますが ”\to”右向き 矢印 と ”\infty”無限大 の 記号を （始めて 出てくるのかな？）使って 下付きの 設定をして 極限の表示 を します。

では TeX ファイル （source code）を見てみます。

\documentclass[a5paper,12pt]{jarticle}
\begin{document}
\begin{displaymath}
\lim_{x\to\infty} f(x)
\end{displaymath}
\end{document}

結果は以下のようになります。

出力

画像は適宜 切り取り 拡大縮小をしていますが

表示の 相違

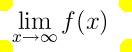
最初に出てきた” In-Line Mathematics”での場合と比べると 異なる表示に なることがわかります。上記の場合は”displaymath”でした。

出力

画像は適宜 切り取り 拡大縮小をしていますが

では TeX ファイル （source code）を見てみます。

\documentclass[a5paper,12pt]{jarticle}
\begin{document}
同じ行の中での表現は $\lim_{x\to\infty} f(x)$ のようになる。
\end{document}

個猫は 昔から 算数は 苦手です この表現が 良いのか は 感知しません！あ と 色々あるようですが この位にしておきます。

にゃんたろう 拝！

2008年 7月28日 (月) 21:01:45 JST 作成

戻る